Siging your app and basic cryptography

Cryptography supports the millions of daily secure internet transactions, for example, in the use of HTTPS, SSH, secure email, secure messaging and eCommerce.

Widespread use of cryptography is made in the Android ecosystem, for example a hash function produces a fingerprint of the app and public-key cryptography is used to generate and use a set of public-private keys in signing and verifying the app.

Specifically, in this lab, we shall sign our MyRent app and explore some simple uses of supporting cyptographic techniques.

Sign MyRent

APK signing

Here we shall build and sign a release version of MyRent.

Use your final version of the app or alternatively download and use a copy from wit-computing GitHub repo: MyRent-15.

Import the project into Android Studio.
In the menu bar, click Build > Generate Signed APK.

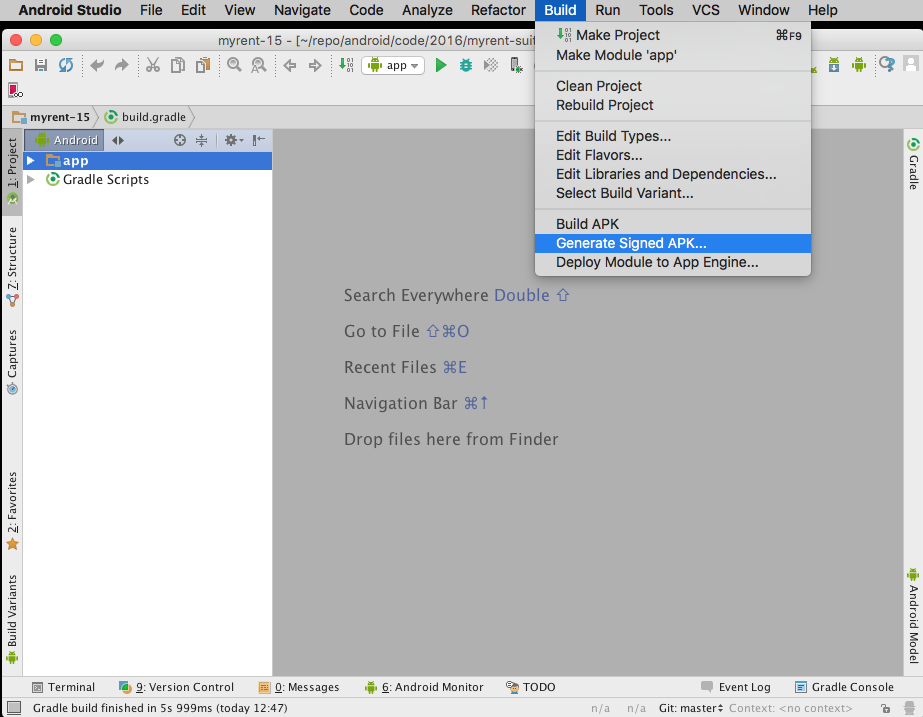
Figure 1: Generate Signed APK

Select the app module from the drop down and click Next.

Figure 2: Select MyRent app module

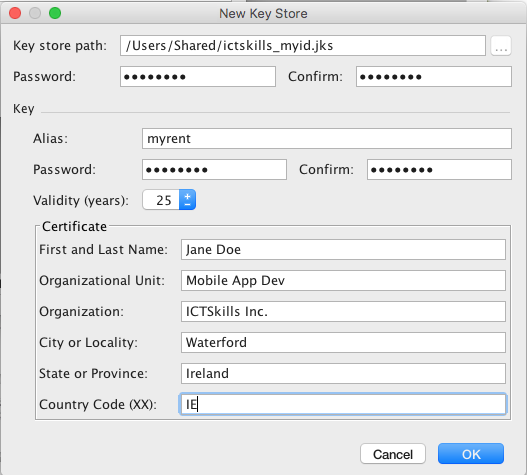
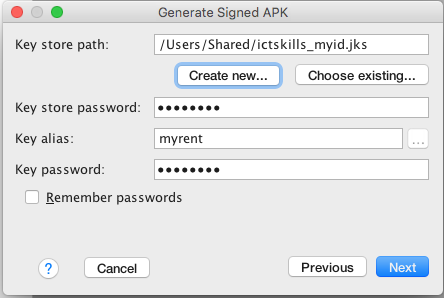
On the New Key Store window, provide the following information for your keystore and key (Figures 3 & 4).

Keystore

Key store path: Select the location where your keystore should be created.
Password: Create and confirm a secure password for your keystore.

Key

Alias: Enter an identifying name for your key.
Password: Create and confirm a secure password for your key. This should be different from the password you chose for your keystore
Validity (years): Set the length of time in years that your key will be valid. Your key should be valid for at least 25 years, so you can sign app updates with the same key through the lifespan of your app.
Certificate: Enter some information about yourself for your certificate. This information is not displayed in your app, but is included in your certificate as part of the APK. Once you complete the form, click OK.

Figure 3: Create a new keystore

Figure 4: New Key Store Sample form

On the Generate Signed APK Wizard window, select a keystore, a private key, and enter the passwords for both. (If you created your keystore in the last step, these fields are already populated for you as shown in Figure 5.) Then click Next.

Figure 5: Generate Signed APK

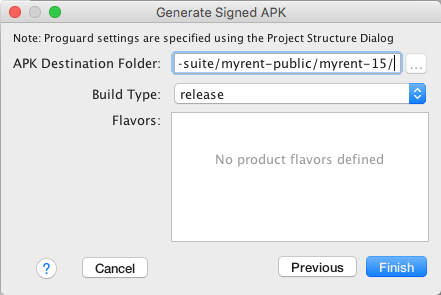
On the next window, select a destination for the signed APK(s) & click Finish. See Figures 6 & 7.

Figure 6: Ready to generate signed APK

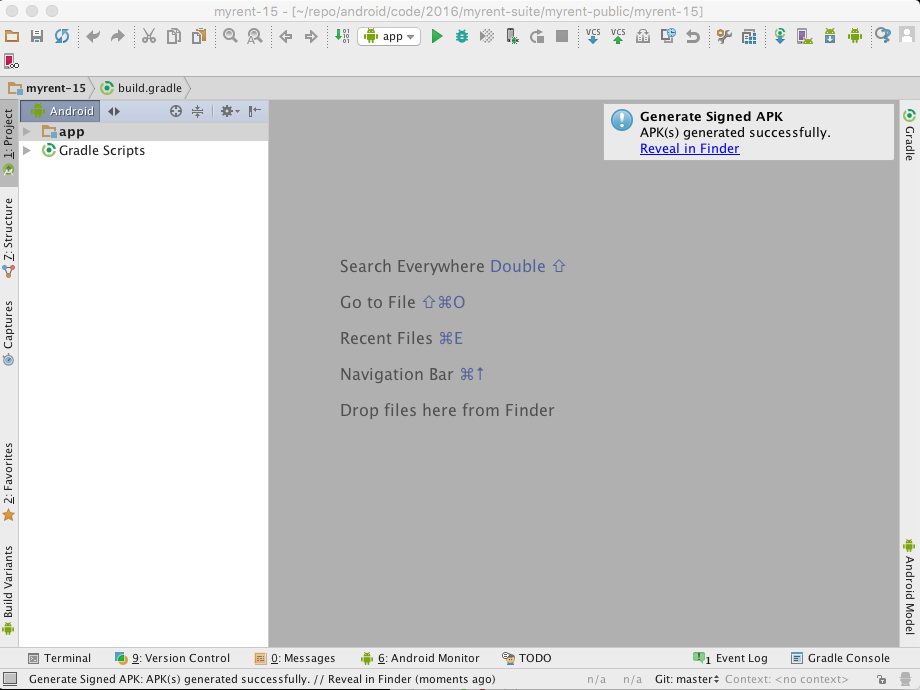
Figure 7: Signed APK successfully generated

Further details are available in the official documentation, for example how to automatically sign the apk, how to include flavours and so on: Sign Your App.

Browse to where the apk is stored on your computer and test by dragging and dropping onto an emulator or installing onto a physical device (tethered to your computer).

You will find instructions on how to publish your app on the Google Play Store in the Google Play Developer Console Help Center

APK verification

In a terminal (OSX) or command prompt (Windows) change into the directory where the recently signed apk resides. Then run this command:

jarsigner -verify -certs app-release.apk

A typical output is shown in Figure 8.

If you require more detail run the command with the -verbose switch.

Figure 8: Verifying Android APK file

To run jarsigner on Windows it is necessary that you:

have installed Java JDK. This is available to download from the Java SE Development Kit 8 Downloads page.
added JDK to path. Instructions are available here: Updating the PATH Environment Variable (Optional)

Hashing

We shall demonstrate the generation of a SHA-1 hash.

Create a Java project in Eclipse IDE named hashing.

In hashing source file create a class named Main:


package hashing;

public class Main {

  public static void main(String[] args) {

  }

}

Download Apache Commons Codec 1.10 file commons-codec-1.10-bin.zip:

Unzip commons-codec-1.10-bin.zip.
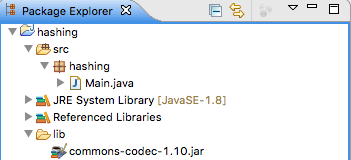
Locate commons-codec-1.10.jar and move to a lib folder in the root of the project as shown in Figure 1.
Select the jar in the navigation panel, right click to open the context menu and add the jar to the build path.

Figure 1: Project structure

Add a method to convert an array of bytes to a hex string:


  public static void byteToHex(byte[] bytes) {
    StringBuilder sb = new StringBuilder();
    for (byte b : bytes) {
        sb.append(String.format("%02X ", b));
    }
    System.out.println(sb.toString());
  }

Import DigestUtils from the Apache Commons Codec jar:


import org.apache.commons.codec.digest.DigestUtils;

Study the DigestUtils JavaDoc. We shall use its sha1 method to obtain the SHA-1 hash of a string in the form of a byte array which we shall then convert and print as the familiar hex string.

Refactor Main:

  public static void main(String[] args) {

    byteToHex(DigestUtils.sha1("ICTSkills_2015"));
    byteToHex(DigestUtils.sha1("ICTSkills_2016"));
  }

Run the program and study the output. It should match that in Figure 2. Observe how very different the two hash values are despite the inputs differing only 1 the last character.

Figure 2: SHA-1 hash values of 2 very similar strings

Now obtain the hash value of a longer string and note that its length is the same as that of each of the earlier strings:


    String lorem = "Lorem ipsum dolor sit amet, consectetur adipiscing elit, "
            + "sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. "
            + "Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris "
            + "nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in "
            + "reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla "
            + "pariatur. Excepteur sint occaecat cupidatat non proident, sunt in "
            + "culpa qui officia deserunt mollit anim id est laborum.";

Figure 3: SHA-1 values of all three strings same length

For reference, here is the complete Main class in which we have moved the contents of main to a method public void sha1():


package hashing;
import org.apache.commons.codec.digest.DigestUtils;

public class Main {

  public static void byteToHex(byte[] bytes) {
    StringBuilder sb = new StringBuilder();
    for (byte b : bytes) {
        sb.append(String.format("%02X ", b));
    }
    System.out.println(sb.toString());
  }

   public static void sha1() {
    byteToHex(DigestUtils.sha1("ICTSkills_2015"));
    byteToHex(DigestUtils.sha1("ICTSkills_2016"));
    String lorem = "Lorem ipsum dolor sit amet, consectetur adipiscing elit, "
            + "sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. "
            + "Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris "
            + "nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in "
            + "reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla "
            + "pariatur. Excepteur sint occaecat cupidatat non proident, sunt in "
            + "culpa qui officia deserunt mollit anim id est laborum.";
    byteToHex(DigestUtils.sha1(lorem));    
  }

  public static void main(String[] args) {

    sha1();
  }

}

Integrity check

In the previous step we downloaded the Apache file commons-codec-1.10-bin.zip available at Download Apache Commons Codec and made use of a contained jar file. However we did not check the integrity of the file. Somehow, during the downloading operation, it could have been possible that the zip file was tampered with. For example commons-codec-1.10.jar might have been replaced with a malicious version containing a keylogger. This would be referred to as a man in the middle attack. (MiTM). To guard against this, the Apache Commons site has provided us with the downloadable zip file's pgp signature and md5 hash. This is shown in Figure 1.

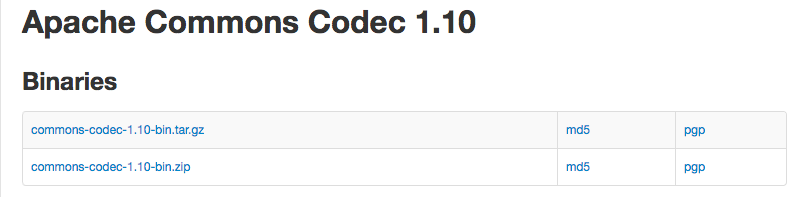
Figure 1: Apache Commons provides md5 hashes and pgp signatures to facilitate verification

We shall verify using both md5 and pgp.

md5 verification

The md5 algorithm produces a 128-bit (16-byte) hash value.

Click on md5 to reveal the hash value for commons-codec-1.10-bin.zip:

59b6046b8cb5bf48c3b2e63bb4424779

We shall now implement a method in our hasing project to calculate the md5 hash value of the downloaded file.

First, download the file guava.jar into the lib folder and add it to the build path.

Next, place the downloaded file commons-codec-1.10-bin.zip in a new folder named zip located in the root of the hashing project. See Figure 2.

Figure 2: Project file structure

Add a method to calculate the hash value:

  public static void md5() {
    File file = new File("./zip/commons-codec-1.10-bin.zip");
    try {
      byte[] data = Files.toByteArray(file);
      byteToHex(DigestUtils.md5(data));
    } catch (IOException e) {
      e.printStackTrace();
    }
  }

These import statements are required:

import java.io.File;
import java.io.IOException;
import com.google.common.io.Files;

Invoke md5(). The output should be similar to that shown in Figure 3. This should match the published hash value (also shown above).

Figure 3: Generated md5 hash value

Several online md5 algorithms are also available some of which you might consider experimenting with.

pgp verification

A requirement is that the GPG Suite or similar application is installed on your computer. In the case of Windows you can use Gpg4win.

Download the suite but before installing verify using the SHA1 signature supplied on the GPG site. You may find the Quick Start Tutorial helpful.

On OSX verification may be performed by changing into the directory where the GPG suite has been saved and running a command similar to the following.

openssl sha1 GPG_Suite-2016.10_v2.dmg

Figure 4: GPG Suite - use SHA1 signature to verify download before installation

This should generate an output similar to that shown in Figure 5. Check this against the published signature.

Figure 5: Verifying GPG installation file

Now download the pgg signature. This will appear as shown in Figure 6. Copy it into a text editor and save it with a .asc extension, for example gpg.asc. Save the file to the same location as the download file that we wish to verify.

Figure 6: PGP Signature

Then run the following verifying command. The output should be something similar to that shown in Figure 7.

gpg --verify gpg.asc commons-codec-1.10-bin.zip

Figure 7: Verification of downloaded file using pgp signature

Further useful information is available at Apache OpenOffice.

Key exchange

Discovered independently by Malcolm Williamson (1973) at GCHQ, England and later by Whitfield Diffie and Martin Hellman (1976). Generally referred to as Diffie-Hellman.

Here is a slide from the presentation decks that describes what we shall now implement in a simple Java program:

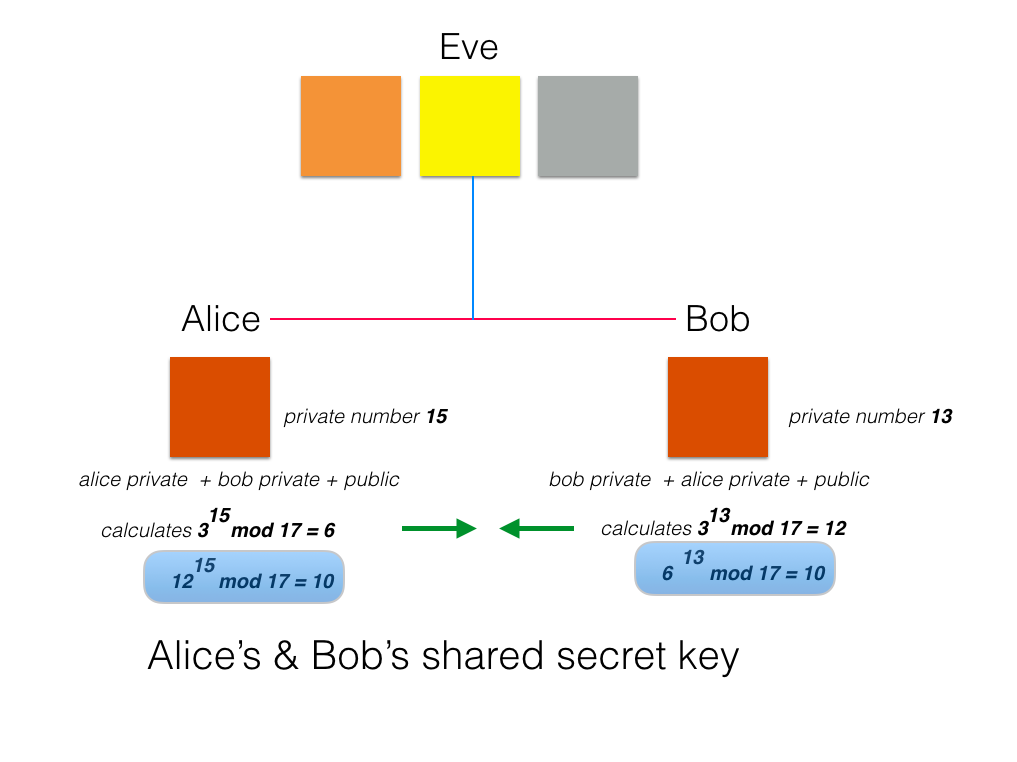
Figure 1: Key exchange illustrated with colours and small prime numbers

In the program we use a type BigInteger because it is suited to modular arithmetic and to cryptography given the very large prime numbers used. Remember that using Math.pow() function to raise a number to an exponent requires parameter types to be doubles. This does not suit modular arithmetic where all types are natural numbers (0, 1, 2, . . .).

Create a project named key_exchange and in a package, also named key_exchange, create two classes, one Alice, the other Bob. The presence of the eavesdropper Eve is implicit and represented by the use of public fields and methods.

Add fields to both classes.


package key_exchange;

import java.math.BigInteger;

public class Alice {

  public static BigInteger Z = BigInteger.valueOf(17); // Modulus
  public static BigInteger g = BigInteger.valueOf(3); // Generator
  private static BigInteger d = BigInteger.valueOf(15); // Alice's private number

}

package key_exchange;

import java.math.BigInteger;

public class Bob {

  public static BigInteger Z = BigInteger.valueOf(17); // Modulus
  public static BigInteger g = BigInteger.valueOf(3); // Generator
  private static BigInteger d = BigInteger.valueOf(13); // Bob's private number

}

We shall now program the equivalent of mixing colours.

Alice and Bob adds their private colours to the public colour.
This is represented mathematically by raising the generator to the power of each person's private number.

In the class Alice:

  public static BigInteger mixedColors() {
    return g.modPow(d, Z); // g raised to power d modulo Z
  }

In the class Bob the code is exactly the same:

  public static BigInteger mixedColors() {
    return g.modPow(d, Z); // g raised to power d modulo Z
  }

The methods are public as the data is transmitted in the clear and so accessible to Eve.

With this information both Alice and Bob are in a position to generate the shared secret key. Here are the methods to do so. Notice the difference between them.

Alice:

  /**
   * Bob's mixed colors + Alice's secret color
   * @return Shared secret key
   */
  private static BigInteger sharedSecretKey() {
    return Bob.mixedColors().modPow(d, Z);
  }

Bob:

  /**
   * Alice's mixed colors + Bob's secret color
   * @return Shared secret key
   */
  private static BigInteger sharedSecretKey() {
    return Alice.mixedColors().modPow(d, Z);
  }

We conclude by adding main methods and printing the secret keys (and additionally the mixed colours).

Alice:

  public static void main(String[] args) {
    System.out.println("Bob's mixed colors " + Bob.mixedColors());
    System.out.println("Alices's shared secret key " + sharedSecretKey());
  }

Bob:

  public static void main(String[] args) {
    System.out.println("Alice's mixed colors " + Alice.mixedColors());
    System.out.println("Bob's shared secret key " + sharedSecretKey());

  }

Run each main function in turn. The expected out is shown in Figure 2.

Figure 2: Alice and Bob now share a secret key. Eve left out in the cold

For reference here are the classes: Alice and Bob.

package key_exchange;

import java.math.BigInteger;

public class Alice {

  public static BigInteger Z = BigInteger.valueOf(17); // Modulus
  public static BigInteger g = BigInteger.valueOf(3); // Generator
  private static BigInteger d = BigInteger.valueOf(15); // Alice's private number

  public static BigInteger mixedColors() {
    return g.modPow(d, Z); // g raised to power d modulo Z
  }

  /**
   * Bob's mixed colors + Alice's secret color
   * @return Shared secret key
   */
  private static BigInteger sharedSecretKey() {
    return Bob.mixedColors().modPow(d, Z);
  }


  public static void main(String[] args) {
    System.out.println("Bob's mixed colors " + Bob.mixedColors());
    System.out.println("Alices's shared secret key " + sharedSecretKey());
  }

}

package key_exchange;

import java.math.BigInteger;

public class Bob {

  public static BigInteger Z = BigInteger.valueOf(17); // Modulus
  public static BigInteger g = BigInteger.valueOf(3); // Generator
  private static BigInteger d = BigInteger.valueOf(13); // Bob's private number

  public static BigInteger mixedColors() {
    return g.modPow(d, Z); // g raised to power d modulo Z
  }

  /**
   * Alice's mixed colors + Bob's secret color
   * @return Shared secret key
   */
  private static BigInteger sharedSecretKey() {
    return Alice.mixedColors().modPow(d, Z);
  }

  public static void main(String[] args) {
    System.out.println("Alice's mixed colors " + Alice.mixedColors());
    System.out.println("Bob's shared secret key " + sharedSecretKey());

  }

}

Public key cryptography

We now implement in Java the very simple public key cryptographic problem presented in the crypto-math slide deck. See slides 29 to 37 inclusive.

Before proceeding it is worth understanding a number of important points regarding public-key cryptography:

A public-private key pair could be considered to be generated by splitting an existing key into complementary keys, one private the other public.
What we mean by private is that the owner of the keys retains this key for his or her personal use, never discloses it to a third party, keeps it safe and protects it with a password to prevent prying eyes from using it should it somehow fall into the wrong hands. We shall not deal with how this is achieved.
The public key is what it implies, public. These often reside on public key servers and are accessible to all.
A message encrypted with the public key can only be decrypted with the associated private key.
A message encrypted with the private key (this is called signing) can be decrypted with the public key (called verification).

Encryption

Create a Java project in Eclipse named key_exchange and a package within the project similarly named.
Create two classes, Alice and Bob.
- Alice shall generate a key pair and:
- Pass the public key from this pair to Bob who shall:
- Encrypt a message using the public key and pass back to Alice.
- Alice shall use her private key to decrypt the message.

We shall use very small prime numbers to facilitate understanding. But in reality, as already pointed out, huge prime numbers are used, numbers that may in some circumstances contain as many as 600 digits (approximately 2000 bits).

Alice:


package public_key_crypto;

import java.math.BigInteger;
/**
 * A class to demonstrate the use of public key cryptography.
 * Two different prime numbers are multiplied to obtain the modulus.
 * The public and private key components, e and d, are supplied only, not calculated.
 * For those interested in the calculation details consult Brit Close course on KhanAcademy.
 * Additionally Eddie Woo has uploaded two very simple YouTube videos dealing with this.
 * Both these are referenced at the foot of one or both accompanying slide decks.
 */
public class Alice {

  // Select 2 prime numbers. In reality 300+ digits long each.
  private static BigInteger p = BigInteger.valueOf(2);
  private static BigInteger q = BigInteger.valueOf(7);

  public static BigInteger Z = p.multiply(q); // Modulus = p x q

  /**
   * Derivation of e & d and relationship between them explained here:
   * @see http://bit.ly/2g9Tyaf
   */
  public static BigInteger e = BigInteger.valueOf(5); // Public exponent used to encrypt
  private static BigInteger d = BigInteger.valueOf(11); // Alice's private key used to decrypt 


}

Bob:

public class Bob {

  /**
   * Public key (e, Z) obtained from Alice
   */
  public BigInteger e; // Encrypting exponent 
  public BigInteger Z; // The  modulus
  private BigInteger message = BigInteger.valueOf(2); // Private plain text message

  /**
   * Create Bob, providing the public key set as parameters.
   * @param e
   * @param Z
   */
  public Bob(BigInteger e, BigInteger Z) {
    this.e = e;
    this.Z = Z;
    System.out.println("Shhhh. Bob here. I know you can keep a secret. The message is " + message);
  }


}

Now add a method to Bob to encrypt a message.

  /**
   * c = m^e mod Z, i.e. m raised to the power of e modulo Z.
   * @return The ciphertext
   */
  public BigInteger encryptMessage() {
    return message.modPow(e, Z);
  }

It only remains for Alice to

Create a Bob instance,
Invoke Bob's method to encrypt Bob's secret message,
Decrypt the encrypted version of Bob's secret message and
Output the results.

All this can be achieved within main as follows:

  public static void main(String[] args) {
    // Instantiate Bob and encrypt his private message
    Bob bob = new Bob(e, Z);
    BigInteger cipherText = bob.encryptMessage();

    //Alice uses her private key to decrypt and output result.
    BigInteger message = cipherText.modPow(d, Z);

    System.out.println("Alice here. See what I've got: ");
    System.out.println("CipherText from Bob: " + cipherText);
    System.out.println("MessageText obtained by decryption of ciphertext: " + message);
  }

Build and run. The output should be similar to that shown in Figure 1.

Figure 1: Public key encryption-decryption

Public Key Cryptography

Signing

In the previous step Bob used Alice's public key to encrypt a message.

Alice then used her private key to decrypt the ciphertext.

Here Alice will send a public message to Bob to which Eve will have access.

What's of concern to both Alice and Bob is not that Eve can read the message but that the author of the message is Alice and no one else.

To ensure this Alice will encrypt the message with her private key. Then Bob, or indeed Eve, can decrypt the message with the public key and in being able to do so can be confident that Alice is the author.

For simplicity the message will comprise a single digit. But it could easily be an indefinite length string. However the additional work would not contribute to the current learning topic.

Add a method to Bob:

  /**
   * Check if signedMessage, when decrypted with public key, matches the message.
   * @param signedMessage The message signed with Alice's private key.
   * @param message The plain text message.
   * @return Returns true if the message author is Alice.
   */
  public boolean verifyMessage(BigInteger signedMessage, BigInteger message) {
    BigInteger unsignedMessage = signedMessage.modPow(e, Z);
    return message.equals(unsignedMessage);
  }

This method uses the public key to decrypt the incoming signed message.

It then compares this unsigned message to the clear text message.

If they are equal then the author is Alice and the boolean true is returned.
Otherwise the return value is false.

Now to Alice. Declare and initialize a field to contain the message. The message is 11:

  public static BigInteger message = BigInteger.valueOf(11);

Sign the message:

/**
   * Sign a message using Alice's private key.
   * This, in effect, is encrypting the message.
   * @return The signed message.
   */
  private static BigInteger signedMessage() {
    return message.modPow(d,  Z);
  }

Alice invokes Bob.verifyMessage to determine if the message Bob has received is the one which she authored.

  /**
   * Invoke Bob.verifyMessage to determine if the author is Alice.
   * Output the result - true if Alice is the author.
   * @param bob An instance of Bob
   */
  private static void verifyMessage(Bob bob) {
    boolean isVerified = bob.verifyMessage(signedMessage(), message);
    System.out.println("Alice message verified? " + isVerified);

  }

Finally, invoke this method in Alice.main. Remember that an instance of Bob already exists in main and we pass this as a parameter:

    verifyMessage(bob);

Figure 1: Message verified

For reference, both completed classes are provided here:

package public_key_crypto;

import java.math.BigInteger;
/**
 * A class to demonstrate the use of public key cryptography.
 * Two different prime numbers are multiplied to obtain the modulus.
 * The public and private key components, e and d, are supplied only, not calculated.
 * For those interested in the calculation details consult Brit Close course on KhanAcademy.
 * Additionally Eddie Woo has uploaded two very simple YouTube videos dealing with this.
 * Both these are referenced at the foot of one or both accompanying slide decks.
 */
public class Alice {

  // Select 2 prime numbers. In reality 300+ digits long each.
  private static BigInteger p = BigInteger.valueOf(2);
  private static BigInteger q = BigInteger.valueOf(7);

  public static BigInteger Z = p.multiply(q); // Modulus = p x q

  /**
   * Derivation of e & d and relationship between them explained here:
   * @see http://bit.ly/2g9Tyaf
   */
  public static BigInteger e = BigInteger.valueOf(5); // Public exponent used to encrypt
  private static BigInteger d = BigInteger.valueOf(11); // Alice's private key used to decrypt 

  public static BigInteger message = BigInteger.valueOf(11);

  /**
   * Sign a message using Alice's private key.
   * This, in effect, is encrypting the message.
   * @return The signed message.
   */
  private static BigInteger signedMessage() {
    return message.modPow(d,  Z);
  }

  /**
   * Invoke Bob.verifyMessage to determine if the author is Alice.
   * Output the result - true if Alice is the author.
   * @param bob An instance of Bob
   */
  private static void verifyMessage(Bob bob) {
    boolean isVerified = bob.verifyMessage(signedMessage(), message);
    System.out.println("Alice message verified? " + isVerified);

  }

  public static void main(String[] args) {
    // Instantiate Bob and encrypt his private message
    Bob bob = new Bob(e, Z);
    BigInteger cipherText = bob.encryptMessage();

    //Alice uses her private key to decrypt and output result.
    BigInteger message = cipherText.modPow(d, Z);

    System.out.println("Alice here. See what I've got: ");
    System.out.println("CipherText from Bob: " + cipherText);
    System.out.println("MessageText obtained by decryption of ciphertext: " + message);

    verifyMessage(bob);
  }

}

package public_key_crypto;

import java.math.BigInteger;

public class Bob {

  /**
   * Public key (e, Z) obtained from Alice
   */
  public BigInteger e; // Encrypting exponent 
  public BigInteger Z; // The  modulus
  private BigInteger message = BigInteger.valueOf(2); // Private plain text message

  /**
   * Create Bob, providing the public key set as parameters.
   * @param e
   * @param Z
   */
  public Bob(BigInteger e, BigInteger Z) {
    this.e = e;
    this.Z = Z;
    System.out.println("Shhhh. Bob here. I know you can keep a secret. The message is " + message);
  }

  /**
   * c = m^e mod Z, i.e. m raised to the power of e modulo Z.
   * @return The ciphertext
   */
  public BigInteger encryptMessage() {
    return message.modPow(e, Z);
  }

  /**
   * Check if signedMessage, when decrypted with public key, matches the message.
   * @param signedMessage The message signed with Alice's private key.
   * @param message The plain text message.
   * @return Returns true if the message author is Alice.
   */
  public boolean verifyMessage(BigInteger signedMessage, BigInteger message) {
    BigInteger unsignedMessage = signedMessage.modPow(e, Z);
    return message.equals(unsignedMessage);
  }

}